Index: |
|
|
|||
|
|
||||
|
|
* ETUDE
* Copyright
(C) 1999 |
Index: |
|
|
|||
|
|
||||
|
|
"ETUDE" est un programme synthétique d'étude de fonctions, qui s'adresse aux lycéens, étudiants et ingénieurs. A cet effet, il
mobilise et coordonne les différents outils de calcul disponibles: Limites, dérivées, résolutions d'équations, graphiques.
L'affichage des résultats, ( limites aux bornes, continuité, dérivabilité, tableaux de variations, branches infinies et asymptotes,
graphique ), est particulièrement soigné et conforme à l'usage et aux programmes de mathématiques de la série scientifique du
Baccalauréat.
On considère une fonction numérique f , définie sur un intervalle (a ; b), ouvert ou fermé, et deux fois dérivable sur l'intervalle ouvert ]a ; b[, sauf éventuellement en k points "singuliers", ( 0<=k<=5 ), notés par ordre croissant s1, s2,...,sk, en chacun desquels la fonction f peut ne pas être définie, continue ou dérivable.
Le programme commence par étudier l'existence d'un prolongement par continuité de f en chacun des points de { a [, s1 , s2 ,..., sk ], b }.
Puis il étudie la fonction f, successivement sur chacun des intervalles (x';x") délimités par les points a [, s1, s2,..., sk ], b, en effectuant à chaque fois les opérations suivantes:
Simplification éventuelle de l'expression f(x) sur l'intervalle d'étude.
Calcul des dérivées d'ordre 1 et 2, f ' et f ", sur l'intervalle d'étude ouvert.
Recherche des zéros de f ' et f " sur l'intervalle d'étude ouvert.
Etude éventuelle de la continuité et de la dérivabilité, aux ordres 1 et 2, aux bornes de l'intervalle d'étude.
Détermination du signe de f ' et f " sur l'intervalle d'étude ouvert.
Détermination complète des variations de f sur l'intervalle d'étude, et affichage du tableau de variations, incluant les signes de f ' et éventuellement de f ".
Le programme choisit ensuite une fenêtre graphique, adaptée à la représentation de f sur l'intervalle (a ; b), puis trace la courbe C de f , en indiquant ses points de discontinuité éventuels.
Le programme étudie, s'il en existe, les branches infinies de la courbe C et détermine les asymptotes qui leur sont éventuellement associées.
Le programme crée un tableau de données, contenant les limites et les valeurs, exactes ou approchées, des fonctions f, f ' et f ", en chacun des points a,[s1,s2,...,sk],b.
Enfin, le programme définit un menu, permettant à l'utilisateur de retrouver et de consulter librement les différents résulats de l'étude de fonction.
Pour télécharger ETUDE pour TI-89 |
Ouvrir l'archive ETUDE89.ZIP à l'aide de Winzip ou d'un logiciel de décompression approprié. Celle-ci contient 2 fichiers et 1 dossier:
- etude89.htm: Cette documentation;
- etude10.89g: Le programme ETUDE;
- Images: Dossier contenant les images de la documentation.Avec le logiciel et le cable TI-GRAPH LINK, copiez le groupe de fichiers "etude10.89g" sur votre calculatrice TI-89.
( Le logiciel TI-GRAPH LINK peut être téléchargé gratuitement sur le site web de Texas-Instruments ).
L'installation crée, (s'ils n'existent pas déjà ), 2 répertoires dans lesquels sont répartis les fichiers du groupe "etude10.89g":
Le répertoire "ETUDE" contient 40 fichiers, occupant au total: 33714 octets pour la TI-89.
Ceux des fichiers qui sont déjà protégés pourront être archivés, car ils ne sont pas modifiés par l'exécution du programme.
Les autres ne doivent pas être archivés !
Le répertoire "SMALLTXT" contient la petite police de caractères, utilisée pour l'écriture des résultats sur l'écran graphique:
81 fichiers, occupant au total: 969 octets.
Les 2 fichiers suivants, occupant au total 264 octets, sont ajoutés au répertoire "MAIN": "expsubst" et "strsubst".
Avant de lancer le programme, placez la calculatrice dans le répertoire "ETUDE".
Vous pouvez maintenant exécuter le programme en tapant "etude( )", et en appuyant sur ENTER.
L'étude de
fonction comporte plusieurs étapes. A la fin de chaque étape,
le programme s'arrête en mode pause; (
l'indicateur de mode [ pause / busy ] est
affiché en bas de l'écran à droite ). Après
avoir consulté les résultats et répondu aux questions
éventuelles, appuyez sur ENTER pour continuer
l'exécution du programme.
NB: Ne pas tenir compte des messages
d'avertissement,( ex: "More solutions may exist",
"Overflow replaced by...",...), qui s'inscrivent
parfois, en bas de l'écran. Les routines de vérification
nécessaires sont incoporées au programme.
Introduction
des données:
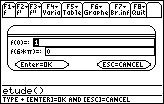
A la première exécution du programme "etude", la calculatrice affiche la fenêtre de dialogue ci-contre. * Sur la 1ère ligne,
tapez l'expression "f(x)"
de la fonction " f " à étudier, en
utilisant obligatoirement la variable x. |
|
||
N.B: Lors des exécutions suivantes du programme "etude", la calculatrice affichera une fenêtre de dialogue contenant les données relatives à la dernière fonction étudiée. Il vous suffira alors de les modifier, en tout ou partie. L'exemple 1, ci-contre, sera utilisé pour illustrer certaines des étapes suivantes: f(x)=x.exp(1/(x+3)). |
|
||
| L'exemple 2, ci-contre, sera également dévelppé dans la suite: f(x)=(x²+x)/(|x²-1|+1). |
|
||
| De même pour l'exemple 3, ci-contre: f(x)=sin(x)/x. |
|
Cette étape, facultative, ne se produit que si l'une des conditions (i) ou (ii) suivantes est réalisée.
Pour chaque point " t ", appartenant à
l'ensemble { a[,s1,s2,...,sk],b}, où s1, s2, ..., sk
désignent les points singuliers de f sur ]a ; b[ rangés
par ordre croissant, la calculatrice effectue la
démarche suivante:
-i) Si le réel f(t) existe, la calculatrice vous propose
de définir f, au point t, par f(t).
-ii) Sinon, et dans le cas où f admet un prolongement
par continuité, en t, à gauche ou à droite, la
calculatrice propose de prendre pour f(t) une valeur
réalisant ce prolongement.
Vous pouvez alors:
- Soit, accepter cette proposition, en appuyant sur ENTER.
- Soit, la refuser, en remplaçant la valeur indiquée
par:
* "undef",( dans ce cas, la fonction sera
considérée comme non définie au point t );
ou
* un réel de votre choix, ( dans ce cas, la fonction
sera définie au point t par le réel choisi ).
Appuyez ensuite deux fois sur ENTER pour
valider votre choix et relancer le programme.
| Dans l'exemple 1, la fonction f initiale n'est pas définie en -3. Mais elle admet en -3, une limite à gauche égale à 0, et une limite à droite égale à moins l'infini. Par suite, f admet un prolongement par continuité à gauche en-3. La calculatrice propose donc de continuer l'étude en prenant, comme fonction f, ce prolongement. Acceptons sa proposition ! |
|
||
| Dans l'exemple 2,
en utilisant l'expression initiale de f(x), les
réels -1 et 1 ont pour images respectives 0 et
2. La calculatrice propose donc de continuer
l'étude de la fonction f, définie sur R,
par: f(x) = (x²+x)/(|x²-1|+1). Acceptons sa proposition ! |
|
||
| Dans l'exemple 3,
en utilisant l'expression initiale de f(x), le
réel 6.PI a pour image 0. D'autre part, la fonction f initiale n'est pas définie en 0, mais elle a en 0 une limite (à droite) égale à 1. Par suite, f admet un prolongement par continuité (à droite) en 0. La calculatrice propose donc de continuer l'étude en prenant, comme fonction f, ce prolongement. Acceptons sa proposition ! |
 |
Calcul
des dérivées première et seconde de f.
* Cette étape est facultative. Elle se produit lorsque les expressions algébriques des dérivées de f sont identiques sur chacun des intervalles ]a;s1[,]s1;s2[,...,]sk;b[, où s1,s2,...,sk désignent les points singuliers éventuels de f, rangés par ordre croissant. Si I désigne l'union des intervalles ]a;s1[,]s1;s2[,...,]sk;b[, la calculatrice affiche alors la dérivée (première) de f sur I, suivie, si l'option <avec f "> a été choisie, de la dérivée seconde de f sur I. * Dans l'exemple 1, on obtient: |
|
||
| * Dans l'exemple 3, on obtient: |
|
| * Dans l'exemple
ci-contre: f(x)=ln|x²-1|,
avec a=-infini, b=+infini et les points
singuliers -1 et 1. Les expressions algébriques des dérivées de f sont effectivement identiques sur chacun des intervalles ]-infini;-1[,]-1;1[ et ]1;+infini[. |
|
Etude
de la fonction f sur l'intervalle (x';x").
S'il
n'existe aucun point singulier sur ]a;b[, l'intervalle
d'étude (x';x") n'est autre que (a;b).
S'il existe k points singuliers sur ]a;b[, l'ensemble des
opérations suivantes est effectué k+1 fois, en prenant
successivement l'intervalle d'étude (x';x") égal
à (a;s1),(s1;s2),...,(sk;b).
4.1 Simplification de
l'expression f(x) sur l'intervalle ]x';x"[.
Cette étape, facultative, se produit dans le cas où f(x) contient une ou plusieurs valeurs absolues, dont l'évaluation est un préalable indispensable au calcul de la dérivée de f sur l'intervalle ]x';x"[.
Les zéros de chaque fonction, située à l'intérieur d'une valeur absolue, sont des points singuliers de f, la dérivabilité de f en ces points n'étant pas assurée. Comme l'intervalle ]x';x"[ ne contient aucun point singulier et que chacune de ces fonctions est continue sur ]x';x"[, elle est de signe constant sur ]x';x"[. Chaque valeur absolue peut donc être effectuée sur l'intervalle ]x';x"[, de façon à simplifier l'expression f(x) sur cet intervalle.
Dans l'exemple 2, la fonction f admet sur R les deux points singuliers -1 et 1, racines du trinôme x²-1 situé à l'intérieur de la valeur absolue. f est donc étudiée successivement sur les intervalles ]-infini;-1], [-1;1] et [1;+infini[. Sur chaque intervalle, la calculatrice commence par donner une expression simplifiée de f(x), en effectuant |x²-1|, selon le signe de x²-1 sur cet intervalle, et en simplifiant éventuellement le quotient obtenu.
|
|
|
4.2 Calcul des dérivées première [et seconde] de f sur l'intervalle ouvert ]x';x"[.
Cette étape est facultative. Elle se produit lorsque l'expression des dérivées dépend de l'intervalle d'étude ]x';x"[.
La calculatrice affiche alors la dérivée (première) de f sur ]x';x"[, suivie, si l'option <avec f "> a été choisie, de la dérivée seconde de f sur ]x';x"[.
Dans l'exemple 2, on obtient:
4.3 Recherche des zéros de f ',[ et de f " ], sur l'intervalle ouvert ]x';x"[.
La calculatrice détermine les zéros ,(valeurs exactes si possible, sinon approchées), de la dérivée première de f, notée f ', sur l'intervalle ouvert ]x';x"[, puis, si l'option <avec f "> a été choisie et après avoir appuyé sur ENTER, elle détermine les zéros de la dérivée seconde de f, notée f ", sur ]x';x"[.
NB: Le nombre total de zéros de f ' et f " ne peut excéder 11. Lorsque cette situation se présente, la calculatrice arrête le programme en indiquant que l'intervalle d'étude (a;b) est trop grand.
* Dans l'exemple 1, on obtient:
* Dans l'exemple 2, on obtient:
Dans l'exemple 3, on obtient:
4.4 Tableau de variation de f sur l'intervalle (x';x").
La calculatrice affiche ensuite le tableau de variations complet de f, sur l'intervalle (x';x").
* Sur la 1ère ligne se trouvent les valeurs remarquables de x, ( bornes x' et x" de l'intervalle d'étude et zéros des dérivées ), en valeurs exaxtes, si possible, sinon désignées par des lettres choisies dans la liste: {j,k,m,n,p,q,r,s,t,u,v}.
* Sur la 2ème ligne se trouvent des valeurs décimales approchées des réels figurant sur la 1ère ligne.
* Si l'option <avec f "> a été choisie à l'étape n°1, la 3ème ligne précise le signe de f ", s'ils existent les nombres dérivés de f à l'ordre 2 en x' et x", respectivement à gauche et à droite, et les images par f " des réels de ]x';x"[ figurant sur la 1ère ligne; (les valeurs indiquées sont exactes, si possible, sinon approchées).
* L'avant-dernière ligne comporte, le signe de f ', s'ils existent les nombres dérivés de f en x' et x", respectivement à gauche et à droite, et les images par f ' des réels de ]x';x"[ figurant sur la 1ère ligne; (les valeurs indiquées sont exactes, si possible, sinon approchées).
* La dernière ligne donne les variations de f : ( Sens de variation, limites en x' et x" respectivement à gauche et à droite, images par f des réels figurant sur la 1ère ligne).
* Dans l'exemple 1, on obtient:
* Dans l'exemple 2, on obtient:
Dans l'exemple 3, on obtient:
Le nombre de réels indiqués sur la 1ère ligne étant supérieur à 7, le tableau de variations de f sur [0;6.PI] est scindé en 2 parties, associées respectivement aux intervalles [0;q] et [q;6.PI]. On obtient le second tableau en appuyant sur ENTER.
Tracé
de la courbe représentative de f sur l'intervalle (a;b).
La programme choisit automatiquement une fenêtre
graphique, adaptée à la courbe représentative de f sur
l'intervalle (a;b).
Il trace ensuite cette courbe en k+1 étapes, la variable
x décrivant succesivement les intervalles:
(a;s1),(s1;s2),...,(sk;b), où s1,s2,...,sk désignent
les points singuliers de f, rangés par ordre croissant,
sur ]a;b[.
Exemple 1: |
Exemple 2: |
Exemple 3: |
|
|
|
Etude
des branches infinies de la courbe représentative de f
et tracé des asymptotes éventuelles.
Cette étape est facultative. Elle se produit lorsque la
courbe représentative de f possède une ou plusieurs
branches infinies.
Pour chaque branche infinie, la calculatrice précise
l'asymptote éventuelle associée ou, s'il s'agit d'une
branche infinie en +infini ou -infini, sa direction
asymptotique. Dans le cas où la courbe admet une ou
plusieurs asymptotes, celles-ci sont ensuite tracées
pour compléter le graphique précédent.
Dans l'exemple 1, on obtient:
|
|
|
|
Dans
l'exemple 2, on obtient:
|
|
|
Encore
un exemple:
|
|
|
|
Emploi du menu utilisateur.
Le programme se termine par
l'affichage, en haut de l'écran HOME, d'un menu
utilisateur, associé aux touches de
fonction suivantes:
- Tapez sur F1, puis 2 fois sur ENTER, pour
envoyer dans la pile, s'il n'y a pas de points
singuliers, l'expression f(x), sinon une liste contenant
les expressions f(x) simplifiées sur chacun des
intervalles (a;s1),(s1;s2),...,(sk;b).
- Tapez sur F2, puis 2 fois sur ENTER,
pour envoyer dans la pile, s'il n'y a pas de points
singuliers, l'expression f '(x) de la dérivée de f,
sinon une liste contenant les expressions f '(x)
simplifiées sur chacun des intervalles
]a;s1[,]s1;s2[,...,]sk;b[.
- Tapez sur F3, puis 2 fois sur ENTER,
pour envoyer dans la pile, si l'option <avec f
"> a été choisie, s'il n'y a pas de points
singuliers, l'expression f "(x) de la dérivée
seconde de f, sinon une liste contenant les expressions f
"(x) simplifiées sur chacun des intervalles
]a;s1[,]s1;s2[,...,]sk;b[.
- Tapez sur F4, puis 2 fois sur ENTER,
pour afficher le tableau de variations, ou, s'il y a
plusieurs tableaux de variations, l'un de ces tableaux
choisi dans une liste.
- Tapez sur F5, puis 2 fois sur ENTER,
pour afficher la table des valeurs, ainsi que des limites
aux bornes et points singuliers éventuels des fonctions
f, f ' et éventuellement f ".NB:
Avant la première utilisation du programme ETUDE, il est
nécessaire de définir la variable data
"valeurs" comme variable data courante, en
tapant: <APPS> 6 2 <ENTER>.
- Tapez sur F6, puis 2 fois sur ENTER,
pour retracer la courbe de f et ses asymptotes, dans la
fenêtre automatique ou la fenêtre courante, ou bien
pour effectuer une finition de la courbe de f
actuellement affichée: Présentation des points d'arrêt
ou de discontinuité, lissage ...
- Tapez sur F7, puis 2 fois sur ENTER,
pour envoyer dans la pile une matrice contenant les
résultats de l'étude des branches infinies de la courbe
de f.
- Tapez sur F8, puis 2 fois sur ENTER,
pour effacer l'environnement du programme ETUDE,
variables et graphique, et pour rétablir les modes et
l'environnement précédents.
Remarques:
-1) Chacune des fonctions précédentes n'est
accessible que lorsque le menu utilisateur (
"CUSTOM" ) est actif. Comme après chaque
opération, la calculatrice revient automatiquement au
menu standard, il faudra rétablir manuellement le menu
utilisateur en tapant: <2nd> 3.
-2) Lorsque l'écran graphique est actif, il
est également possible d'utiliser les fonctions du menu
graphique standard, ( F2=Zoom,
F3=Trace, F4=ReGraph,
F5=Math, F6=Draw,
F7 ), pour compléter le graphique ou pour effectuer
certains calculs en liaison avec la courbe de f.
Version 1.0, ( première version publique ), mise à disposition sur http://users.aol.com/mimoun36/home.htm, le 5 novembre 1999.
Les encouragements ou les critiques,
éventuellement accompagnés de propositions visant à améliorer
ce programme, seront les bienvenus.
Mon email : mimoun36@aol.com
( Michel MOUNET )
Mon site web: http://users.aol.com/mimoun36/home.htm